
벡터와 스칼라(가중치)의 곱으로 이루어진 덧셈 연산을 선형결합(벡터 방정식)이라고 한다
벡터 방정식을 이용해서 해가 있는지 따져볼 수 있다

span : 재료 벡터를 가지고 만들 수 있는 모든 선형결합(벡터)의 집합
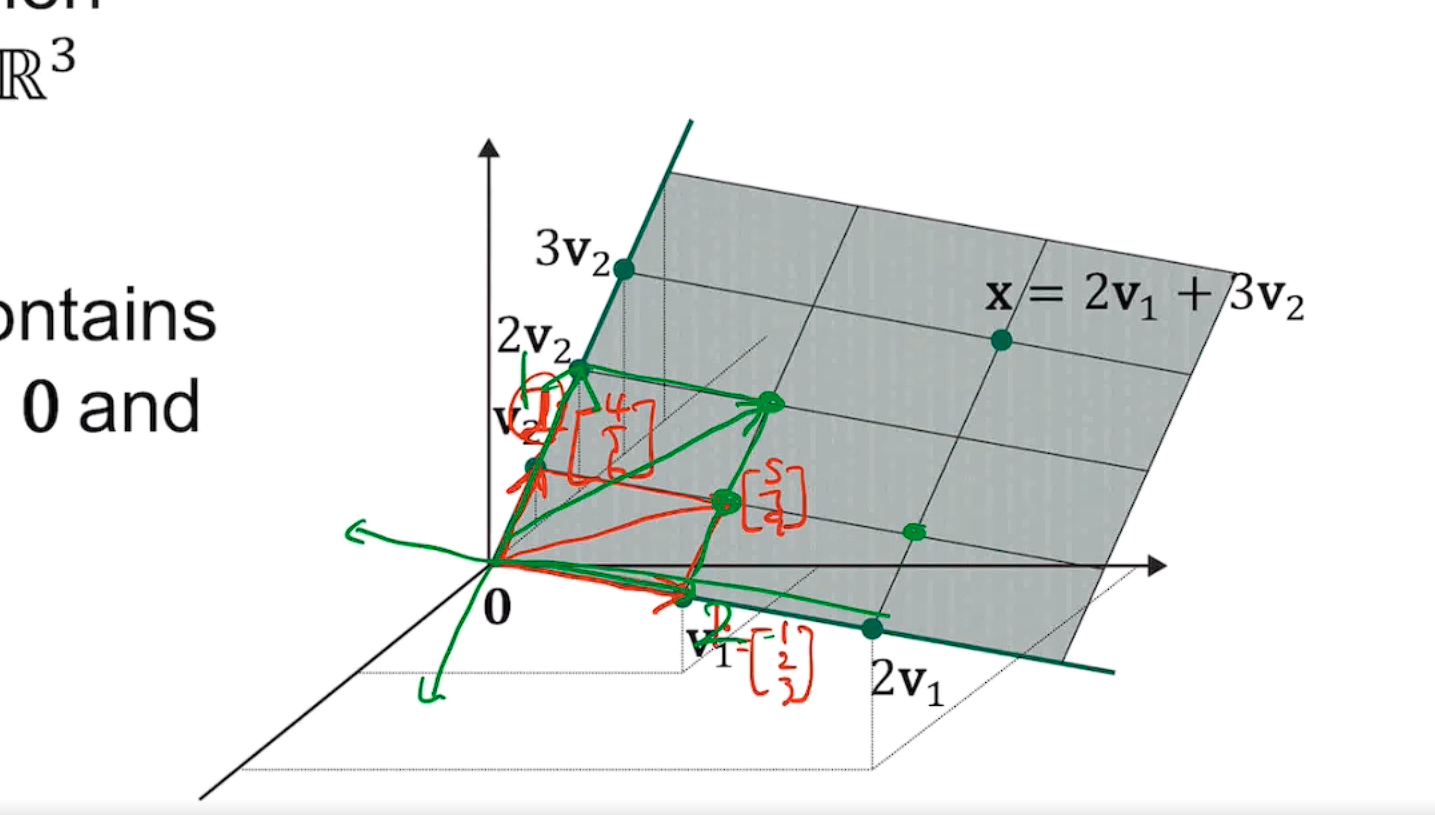
두 벡터가 선형결합을 통해 만들어내는 평면(무수히 많은 벡터들)을 span이라고 한다
만약 1개의 벡터를 고려한다면 '선'이 되는 것이고
2개의 벡터라면 '면' , 3개라면 '공간'이 되는 것이다
이 선,면,공간 모두 span이라고 부른다 (물론 4,5,6개... 도 가능하겠지?)

3개의 재료벡터와 미지수 x(가중치)의 선형결합으로 가능한 모든 경우(span)을 만들어 봤을때 그 span에 우항의 벡터가 포함되어 있다면 해(x1,x2,x3)가 있는 것이고 그렇지 않다면 해가 없는 것이다
재료 벡터의 요소 갯수가 차원을 의미하므로 만약 요소가 10개라면 10차원인것이고, 10차원에서 3개의 가중치(3차원)만을 고려한 span을 그린다면 드넓은 우주에 얇은 평면하나 그리는것과 비슷할 것이다
당연히 이런 경우에는 우항의 벡터가 운좋게도 그 평면(span)에 쏙! 포함될 가능성은 낮다고 볼 수 있다
(어렵다 어려워)

기존의 매트릭스 곱을 확장해서 생각해보면, 상수(a,b,c,d)였던 자리에 벡터를 넣는다는 개념을 떠올릴 수 있다
소감
어렵다... 어려워... ai가 대학원을 가야한다는 이유를... 이제서야... 알것...가..ㅌ..수학과 친구들이 잘하겠네...
자료,강의
https://www.boostcourse.org/onlyboostcampaitech6/lecture/1502901/?isDesc=false
'네이버 부스트캠프(naver boostcamp)' 카테고리의 다른 글
| [부스트캠프 AI Tech 프리코스] 11강 선형방정식과 선형시스템 (0) | 2023.08.26 |
|---|---|
| [부스트캠프 AI Tech 프리코스] 10강 경사하강법(순한맛) (0) | 2023.08.25 |
| [부스트캠프 AI Tech 프리코스] 9강 행렬이 뭐에요? (0) | 2023.08.25 |
| [부스트캠프 AI Tech 프리코스] 8강 벡터가 뭔가요? (0) | 2023.08.24 |
| [부스트캠프 AI Tech 프리코스] 7강 numpy (0) | 2023.08.24 |